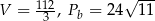Zadanie nr 1807769
Dany jest ostrosłup prawidłowy czworokątny  o podstawie
o podstawie  . Krawędź boczna tego ostrosłupa jest o
. Krawędź boczna tego ostrosłupa jest o 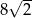 dłuższa od krawędzi podstawy, a wysokość ostrosłupa jest równa 14. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
dłuższa od krawędzi podstawy, a wysokość ostrosłupa jest równa 14. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
Rozwiązanie
Rozpoczynamy od rysunku.
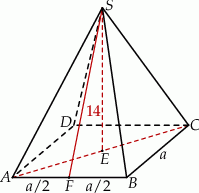
Jeżeli oznaczymy przez  długość krawędzi podstawy, to przekątna podstawy ma długość
długość krawędzi podstawy, to przekątna podstawy ma długość 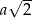 , a krawędź boczna ma długość
, a krawędź boczna ma długość 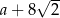 . Piszemy teraz twierdzenie Pitagorasa w trójkącie
. Piszemy teraz twierdzenie Pitagorasa w trójkącie 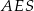 .
.
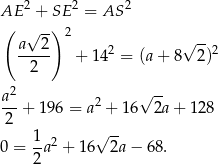
Rozwiązujemy otrzymane równanie kwadratowe.
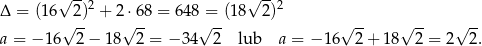
Objętość ostrosłupa jest więc równa
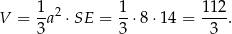
Aby obliczyć pole powierzchni bocznej, obliczamy długość wysokości 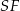 ściany bocznej. Patrzymy na trójkąt prostokątny
ściany bocznej. Patrzymy na trójkąt prostokątny 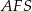 .
.
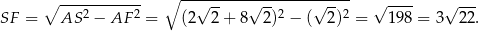
Pole powierzchni bocznej jest więc równe
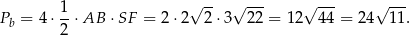
Odpowiedź: