Zadanie nr 1835457
Podstawą graniastosłupa 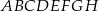 jest prostokąt
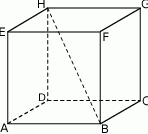
jest prostokąt 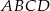 (zobacz rysunek), którego dłuższy bok ma długość 6. Przekątna prostokąta
(zobacz rysunek), którego dłuższy bok ma długość 6. Przekątna prostokąta 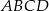 tworzy z jego krótszym bokiem kąt
tworzy z jego krótszym bokiem kąt 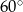 . Przekątna
. Przekątna 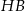 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 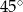 stopni. Oblicz objętość tego graniastosłupa.
stopni. Oblicz objętość tego graniastosłupa.
Rozwiązanie
Zacznijmy od zaznaczenia na rysunku podanych kątów.
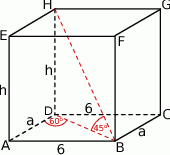
Z trójkąta prostokątnego 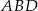 obliczamy długość
obliczamy długość  drugiej krawędzi podstawy.
drugiej krawędzi podstawy.
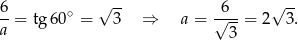
Obliczmy jeszcze długość przekątnej podstawy
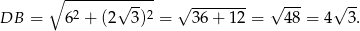
Z trójkąta prostokątnego 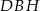 obliczamy długość wysokości graniastosłupa.
obliczamy długość wysokości graniastosłupa.
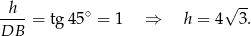
Pozostało obliczyć objętość graniastosłupa.
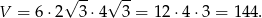
Odpowiedź: 144

