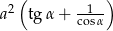Zadanie nr 1849335
Podstawą ostrosłupa jest kwadrat o boku 
. Dwie sąsiednie ściany boczne ostrosłupa są prostopadłe do płaszczyzny podstawy, a dwie pozostałe ściany boczne tworzą z podstawą kąt 
. Oblicz pole powierzchni bocznej ostrosłupa.
Rozwiązanie
Zaczynamy od rysunku.
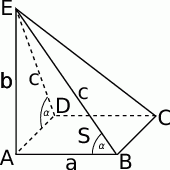
Najważniejsze w tym zadaniu, to zauważyć, że kąty nachylenia ścian bocznych, które nie są prostopadłe do podstawy, to kąty ostre w trójkątach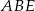 
i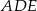 
. Ponadto trójkąty 
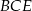i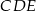 
są prostokątne (bo krawędź 
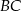jest prostopadła do ściany 
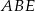, a krawędź 
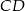do ściany 
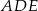). Jak już to wiemy, to zostały proste rachunki.
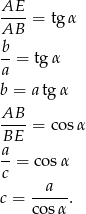
Pozostało policzyć szukane pole powierzchni bocznej
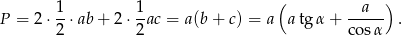
Odpowiedź: 
