Zadanie nr 1852946
Trójkąt o bokach 3, 5, 7 jest podstawą graniastosłupa prostego, w który wpisano kulę. Oblicz objętość tego graniastosłupa.
Rozwiązanie
Przede wszystkim musimy sobie dobrze wyobrazić opisaną sytuację (rysunek).
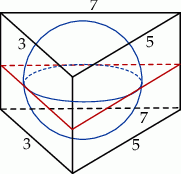
Intuicyjnie powinno być jasne, że informacja o tym, że w graniastosłup jest wpisana kula, daje nam informację o wysokości tego graniastosłupa. Dokładniej rzecz biorąc, rozmiar tej kuli jest wyznaczony przez ściany boczne (a więc tak naprawdę przez trójkąt w podstawie), a wysokość graniastosłupa to średnica kuli. Zastanówmy się jeszcze jak dokładnie trójkąt w podstawie wyznacza rozmiar kuli. Jeżeli zrzutujemy tę kulę na płaszczyznę podstawy, lub przetniemy ten graniastosłup poziomą płaszczyzną na poziomie punktów styczności z kulą, to staje się jasne, że promień  kuli to dokładnie promień okręgu wpisanego w trójkąt w podstawie.
kuli to dokładnie promień okręgu wpisanego w trójkąt w podstawie.
Po tej dokładnej analizie rozwiązanie jest już proste. Pole podstawy liczymy ze wzoru Herona 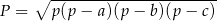 , gdzie
, gdzie 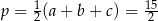 . Wysokość (czyli
. Wysokość (czyli 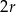 ) obliczymy ze wzoru na pole
) obliczymy ze wzoru na pole 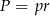 . Liczymy
. Liczymy
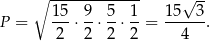
Liczymy teraz  .
.
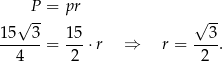
Liczymy objętość
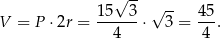
Odpowiedź: