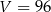/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1869139

Dodaj do ulubionych
Dodaj do rozwiązanych

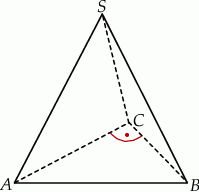
Podstawą ostrosłupa trójkątnego 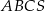ABCS jest trójkąt prostokątny 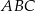ABC , w którym 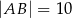|AB | = 10 . Stosunek długości przyprostokątnej 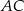AC tego trójkąta do długości przyprostokątnej 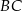BC jest równy 4:3. Wszystkie krawędzie boczne ostrosłupa mają długość 13. Oblicz objętość tego ostrosłupa.

PIC

Rozwiązanie

Dorysujmy wysokość 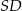SD ostrosłupa.

PIC

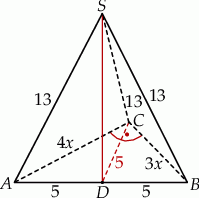
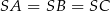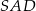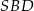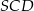Ponieważ SA = SB = SC , trójkąty prostokątne SAD , SBD i SCD są parami przystające (bo każde dwa mają po dwa boki tej samej długości). W takim razie

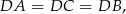
DA = DC = DB ,

czyli spodek wysokości 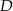D jest środkiem okręgu opisanego na trójkącie prostokątnym 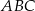ABC . Środek okręgu opisanego na trójkącie prostokątnym to dokładnie środek przeciwprostokątnej (przyprostokątna jest średnicą tego okręgu). Zatem punkt 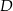D jest środkiem przeciwprostokątnej 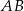AB i

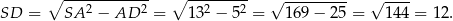
∘ ------------ ∘ --------- √ --------- √ ---- SD = SA 2 − AD 2 = 132 − 52 = 169 − 25 = 144 = 12 .

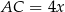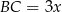Pozostało obliczyć pole trójkąta w podstawie. Jeżeli oznaczymy AC = 4x i BC = 3x , to stosując twierdzenie Pitagorasa w trójkącie 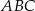ABC mamy

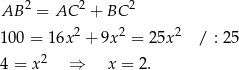
2 2 2 AB = AC + BC 100 = 16x 2 + 9x 2 = 25x 2 / : 25 4 = x2 ⇒ x = 2.

Objętość ostrosłupa jest więc równa

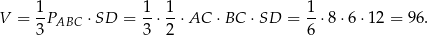
1 1 1 1 V = -PABC ⋅ SD = --⋅--⋅AC ⋅BC ⋅SD = --⋅8⋅6 ⋅12 = 96. 3 3 2 6

 
Odpowiedź: V = 96

Wersja PDF