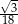/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1879043

Dodaj do ulubionych
Dodaj do rozwiązanych

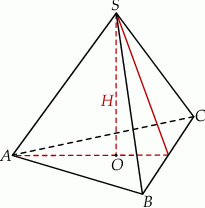
Objętość ostrosłupa prawidłowego trójkątnego 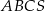ABCS (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie 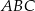ABC tego ostrosłupa jest równy 2. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.

PIC

Rozwiązanie

Dorysujmy wysokość ściany bocznej.

PIC

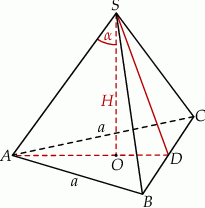
Promień 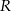R okręgu wpisanego w podstawę to 23 wysokości trójkąta w podstawie, więc jeżeli przez a oznaczymy długość krawędzi podstawy to mamy równanie

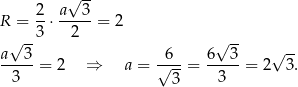
√ -- 2 a 3 R = --⋅ -----= 2 √ -3 2 √ -- a--3- √6-- 6--3- √ -- 3 = 2 ⇒ a = 3 = 3 = 2 3.

Możemy teraz wykorzystać informację o objętości ostrosłupa do obliczenia długości jego wysokości

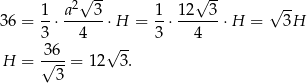
-- -- 1 a2√ 3 1 1 2√ 3 √ -- 36 = -⋅ ------⋅H = --⋅------ ⋅H = 3H 3 4 3 4 H = 3√6--= 12√ 3-. 3

Pozostało teraz obliczyć żądany tangens.

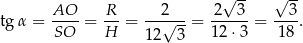
√ -- √ -- AO R 2 2 3 3 tg α = SO-- = H- = --√---= 12-⋅3-= 18-. 12 3

 
Odpowiedź: √ 3 -18

Wersja PDF