/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1923568

Dodaj do ulubionych
Dodaj do rozwiązanych

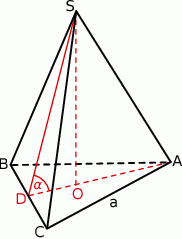
Podstawą ostrosłupa prawidłowego trójkątnego 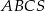ABCS jest trójkąt równoboczny 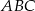ABC . Wysokość 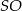SO tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 27. Oblicz pole powierzchni bocznej ostrosłupa 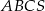ABCS oraz cosinus kąta, jaki tworzą wysokość ściany bocznej i płaszczyzna podstawy ostrosłupa.

Rozwiązanie

Oznaczmy przez a długość krawędzi podstawy ostrosłupa.

PIC

Pole podstawy jest równe 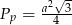2√ - Pp = a4-3 , a wysokość trójkąta w podstawie jest równa

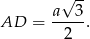
√ -- a--3- AD = 2 .

Wiemy ponadto, że 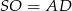SO = AD , więc z podanej objętości ostrosłupa możemy obliczyć a .

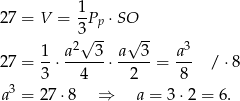
1- 27 = V = 3 Pp ⋅ SO 2√ -- √ -- 3 27 = 1-⋅ a---3⋅ a--3-= a-- / ⋅8 3 4 2 8 a3 = 27 ⋅8 ⇒ a = 3 ⋅2 = 6.

Mamy zatem

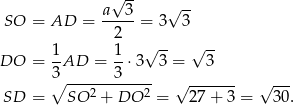
√ -- a 3 √ -- SO = AD = -----= 3 3 2 -- -- DO = 1AD = 1-⋅3 √ 3 = √ 3 3 3 ∘ ---2-------2 √ ------- √ --- SD = SO + DO = 27 + 3 = 30 .

Pole powierzchni bocznej jest więc równe

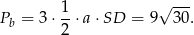
1 √ --- Pb = 3 ⋅--⋅a ⋅SD = 9 3 0. 2

Obliczamy jeszcze cosinus kąta 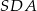SDA .

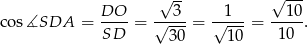
√ -- √ --- DO 3 1 10 cos∡SDA = ----= √----= √----= ----. SD 30 10 10

 
Odpowiedź: 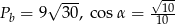√ --- √-- Pb = 9 30, cosα = -1100- .

Wersja PDF