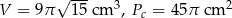/Szkoła średnia/Geometria/Stereometria

Zadanie nr 2063396

Dodaj do ulubionych
Dodaj do rozwiązanych

Powierzchnia boczna stożka jest po rozwinięciu ćwiartką koła o promieniu 12 cm. Oblicz pole powierzchni całkowitej i objętość tego stożka.

Rozwiązanie

Zaczynamy od rysunku.

PIC

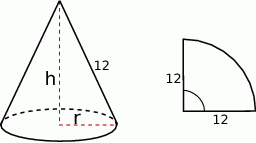
Zauważmy, że z podanych informacji wynika, że tworząca stożka ma długość 12. Ponadto, długość ćwiartki okręgu o promieniu 12 jest równa

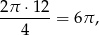
2π--⋅12 4 = 6 π,

co pozwala obliczyć promień podstawy stożka, bo obliczona długość to dokładnie długość okręgu w podstawie stożka. Mamy więc

2πr = 6π ⇒ r = 3.

To z kolei pozwala obliczyć wysokość stożka

∘ -------- ∘ -------- ∘ ------- √ --- h = 122 − r2 = 122 − 9 = 3 42 − 1 = 3 15.

Liczymy teraz objętość i pole powierzchni całkowitej

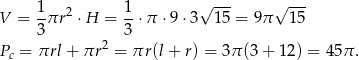
1- 2 1- √ --- √ --- V = 3πr ⋅H = 3 ⋅π ⋅9⋅ 3 15 = 9π 15 2 Pc = πrl + πr = πr(l + r) = 3π (3+ 12) = 45π .

 
Odpowiedź: √ --- V = 9π 15 cm 3, Pc = 45π cm 2

Wersja PDF