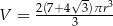Zadanie nr 2183727
Trzy parami styczne kule o promieniach równych 
znajdują się w walcu w ten sposób, że każda z kul jest styczna do obu podstaw walca, oraz do jego powierzchni bocznej. Oblicz objętość walca.
Rozwiązanie
Szkicujemy walec w widoku z boku i z góry.
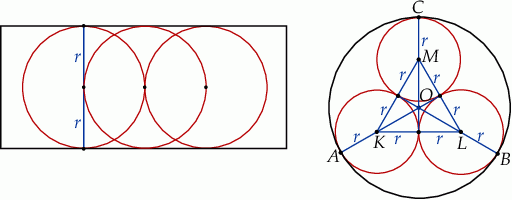
Z obrazka widać, że wysokość walca jest równa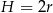 
, więc zadanie sprowadza się do wyznaczenia promienia jego podstawy. W tym celu patrzymy na walec z góry. Na tym obrazku widać, że środki wpisanych kul tworzą trójkąt równoboczny o boku długości 
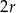. Zatem promień podstawy walca możemy obliczyć korzystając ze wzoru na wysokość trójkąta równobocznego.
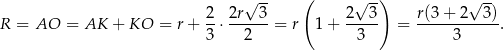
Liczymy objętość walca.
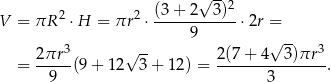
Odpowiedź: 
