/Szkoła średnia/Geometria/Stereometria

Zadanie nr 2247266

Dodaj do ulubionych
Dodaj do rozwiązanych

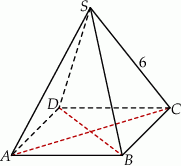
Dany jest ostrosłup prawidłowy czworokątny 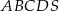ABCDS , którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 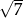√ 7- . Oblicz objętość tego ostrosłupa.

PIC

Rozwiązanie

Przyjmijmy oznaczenia z rysunku.

PIC

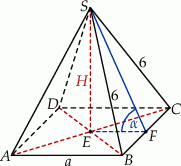
Z trójkąta prostokątnego 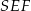SEF mamy

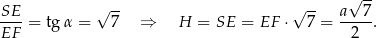
√ -- SE- = tg α = √ 7- ⇒ H = SE = EF ⋅√ 7-= a--7. EF 2

Piszemy twierdzenie Pitagorasa w trójkącie 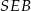SEB .

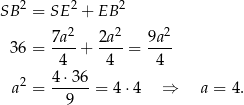
2 2 2 SB = SE + EB 7a 2 2a2 9a2 36 = ----+ ----= ---- 4 4 4 a2 = 4-⋅36-= 4⋅ 4 ⇒ a = 4. 9

Stąd

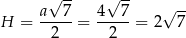
√ -- √ -- a--7- 4--7- √ -- H = 2 = 2 = 2 7

i objętość ostrosłupa jet równa

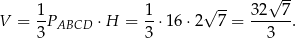
√ -- 1- 1- √ -- 32--7- V = 3PABCD ⋅H = 3 ⋅ 16⋅2 7 = 3 .

 
Odpowiedź: √ - 32--7 3

Wersja PDF