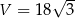/Szkoła średnia/Geometria/Stereometria

Zadanie nr 2267551

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz objętość ostrosłupa prawidłowego czworokątnego jeśli jego krawędź boczna o długości 6 nachylona jest do płaszczyzny podstawy pod kątem 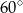60 ∘ .

Rozwiązanie

Zacznijmy od rysunku.

PIC

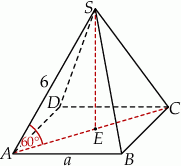
Sposób I

Z trójkąta prostokątnego 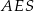AES wyliczamy wysokość 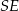SE ostrosłupa oraz odcinek AE .

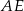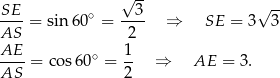
√ -- SE-- ∘ --3- √ -- AS = sin 60 = 2 ⇒ SE = 3 3 AE 1 ----= cos60∘ = -- ⇒ AE = 3. AS 2

Ponieważ w podstawie jest kwadrat, mamy

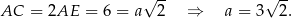
√ -- √ -- AC = 2AE = 6 = a 2 ⇒ a = 3 2.

Liczymy teraz objętość ostrosłupa.

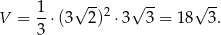
1 √ --2 √ -- √ -- V = --⋅(3 2) ⋅3 3 = 18 3. 3

Sposób II

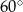Tym razem od razu zauważmy, że trójkąt ACS jest równoramienny z kątem przy podstawie ∘ 6 0 . Jest on więc równoboczny. Zatem

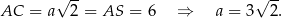
√ -- √ -- AC = a 2 = AS = 6 ⇒ a = 3 2.

Wysokość ostrosłupa możemy wyliczyć ze wzoru na wysokość w trójkącie równobocznym.

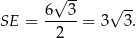
√ -- -- SE = 6--3-= 3 √ 3. 2

Objętość liczymy jak poprzednio.  
Odpowiedź: √ -- V = 18 3

Wersja PDF