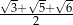Zadanie nr 2324875
Punkty 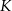 i
i 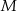 są środkami krawędzi
są środkami krawędzi 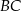 i
i 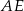 sześcianu
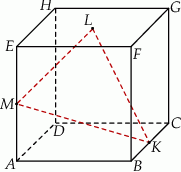
sześcianu 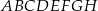 o krawędzi długości 1. Punkt
o krawędzi długości 1. Punkt 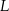 jest środkiem ściany
jest środkiem ściany 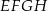 (zobacz rysunek). Oblicz obwód trójkąta
(zobacz rysunek). Oblicz obwód trójkąta 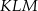 .
.
Rozwiązanie
Niech 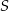 będzie środkiem krawędzi
będzie środkiem krawędzi 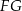 i dorysujmy odcinki
i dorysujmy odcinki 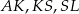 i
i 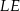 .
.
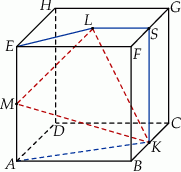
Otrzymaliśmy w ten sposób trzy trójkąty prostokątne 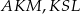 i
i 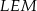 . W każdym z nich liczymy z twierdzenia Pitagorasa długość przeciwprostokątnej.
. W każdym z nich liczymy z twierdzenia Pitagorasa długość przeciwprostokątnej.
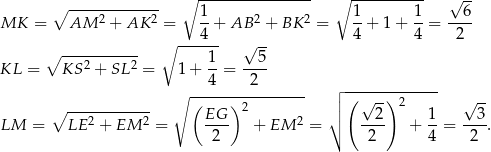
Obwód trójkąta 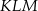 jest więc równy
jest więc równy
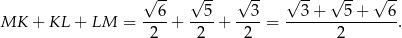
Odpowiedź: