Zadanie nr 2330667
Na środkowej 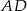 podstawy
podstawy 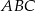 ostrosłupa trójkątnego
ostrosłupa trójkątnego 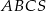 wybrano punkty
wybrano punkty 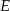 i
i 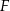 w ten sposób, że
w ten sposób, że 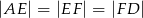 . Przez punkty
. Przez punkty 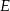 i
i 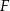 poprowadzono płaszczyzny równoległe do ściany
poprowadzono płaszczyzny równoległe do ściany 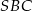 . Oblicz stosunek pól otrzymanych w ten sposób przekrojów ostrosłupa.
. Oblicz stosunek pól otrzymanych w ten sposób przekrojów ostrosłupa.
Rozwiązanie
Szkicujemy opisaną sytuację.
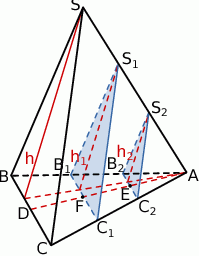
Sposób I
Przy oznaczeniach z rysunku, czworościany 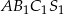 i
i 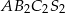 są podobne w skali
są podobne w skali
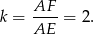
W takim razie
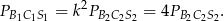
Sposób II
Jeżeli oznaczymy przez 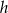 wysokość trójkąta
wysokość trójkąta 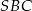 opuszczoną na krawędź
opuszczoną na krawędź 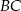 oraz
oraz 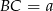 , to
, to
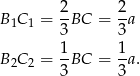
Podobnie wysokości 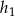 i
i 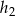 trójkątów
trójkątów 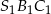 i
i 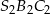 opuszczone na podstawy
opuszczone na podstawy 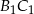 i
i 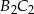 spełniają
spełniają
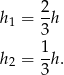
W takim razie
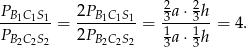
Odpowiedź: 4 : 1

