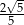/Szkoła średnia/Geometria/Stereometria

Zadanie nr 2380800

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości wszystkich krawędzi ostrosłupa czworokątnego prawidłowego są równe a . Przez wierzchołek ostrosłupa i środki dwóch sąsiednich krawędzi podstawy poprowadzono płaszczyznę . Wyznacz sinus kąta nachylenia wyznaczonego przekroju do podstawy ostrosłupa.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

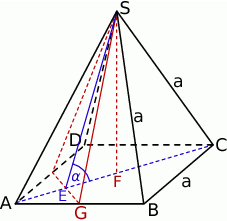
Z trójkąta prostokątnego 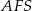AF S obliczamy długość wysokości ostrosłupa.

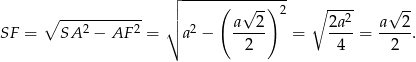
┌│ -----(------)-- ∘ ---- ∘ ------------ │ a √ 2- 2 2a2 a√ 2- SF = SA 2 − AF 2 = ∘ a 2 − ----- = ----= -----. 2 4 2

Długość odcinka 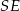SE obliczymy na dwa sposoby.

Sposób I

Ponieważ 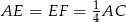1 AE = EF = 4AC , długość odcinka 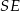SE możemy obliczyć z trójkąta prostokątnego SEF .

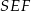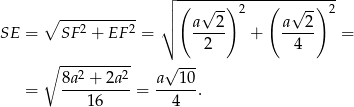
┌ ---------------------- ∘ ----------- ││ ( √ --) 2 ( √ --) 2 SE = SF 2 + EF2 = ∘ a--2- + a--2- = 2 4 ∘ ---------- √ --- 8a-2 +-2a-2 a--10- = 16 = 4 .

Interesujący nas sinus jest więc równy

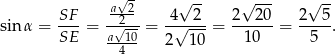
√- √ -- √ --- √ -- SF a-2- 4 2 2 20 2 5 sinα = --- = --2√-- = -√----= ------= ----. SE a410- 2 10 10 5

Sposób II

Ponieważ 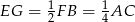EG = 1F B = 1 AC 2 4 , długość odcinka 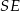SE możemy obliczyć z trójkąta prostokątnego EGS .

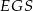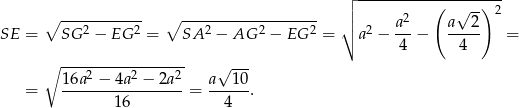
┌ -------------------- │ ( √ -) 2 ∘ ---2------2- ∘ ---2-------2------2 │∘ 2 a-2 a--2- SE = SG − EG = SA − AG − EG = a − 4 − 4 = ∘ ----------------- √ --- 16a2 − 4a2 − 2a2 a 10 = -----------------= ------. 16 4

Sinus kąta nachylenia obliczamy tak samo jak w pierwszym sposobie.  
Odpowiedź: √ - 2--5 5

Wersja PDF