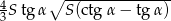/Szkoła średnia/Geometria/Stereometria

Zadanie nr 2421492

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole ściany bocznej ostrosłupa prawidłowego czworokątnego jest równe 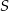S . Kąt płaski przy wierzchołku ostrosłupa ma miarę 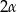2α . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

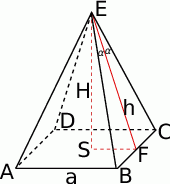
Przyjmując oznaczenia jak na rysunku mamy

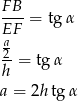
FB- = tg α EF a2- h = tg α a = 2h tg α

Korzystamy teraz z podanego pola ściany bocznej

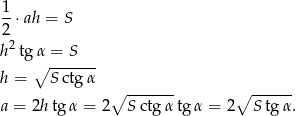
1 --⋅ah = S 2 h2tg α = S ∘ ------- h = Sctg α ∘ ------- ∘ ------ a = 2h tgα = 2 S ctgα tgα = 2 S tgα .

Liczymy teraz wysokość H ostrosłupa

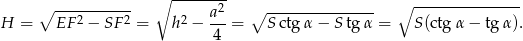
-------- ∘ ----------- ∘ a2 ∘ --------------- ∘ --------------- H = EF 2 − SF 2 = h2 − ---= Sctg α− S tg α = S(ctgα − tg α). 4

Pozostało policzyć szukną objętość

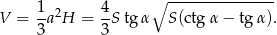
1 4 ∘ --------------- V = -a 2H = -S tgα S(ctg α− tgα). 3 3

 
Odpowiedź: 4 ∘ --------------- 3 Stg α S (ctg α − tgα )

Wersja PDF