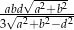Zadanie nr 2742860
Podstawą ostrosłupa 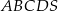 jest prostokąt
jest prostokąt 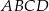 o bokach długości
o bokach długości  i
i 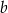 . Krawędź
. Krawędź 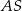 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 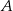 od krawędzi
od krawędzi 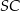 jest równa
jest równa 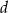 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
Rozwiązanie
Szkicujemy opisaną sytuację.
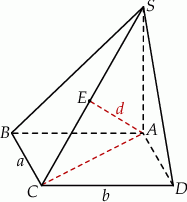
Zadanie oczywiście sprowadza się do obliczenia wysokości ostrosłupa, czyli długości krawędzi 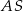 . Niech
. Niech 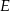 będzie rzutem punktu
będzie rzutem punktu 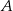 na krawędź
na krawędź 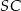 . Długość krawędzi
. Długość krawędzi 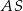 możemy obliczyć licząc pole trójkąta prostokątnego
możemy obliczyć licząc pole trójkąta prostokątnego 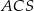 na dwa sposoby (lub, jeżeli ktoś woli, korzystając z podobieństwa trójkątów
na dwa sposoby (lub, jeżeli ktoś woli, korzystając z podobieństwa trójkątów 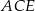 i
i 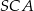 ).
).
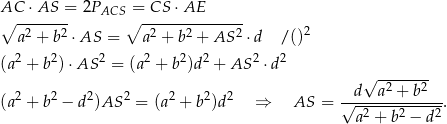
Objętość ostrosłupa jest więc równa
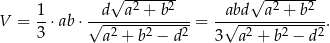
Odpowiedź: