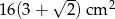/Szkoła średnia/Geometria/Stereometria

Zadanie nr 2828689

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą graniastosłupa prostego jest trójkąt prostokątny równoramienny. Kąt między przekątnymi, wychodzącymi z tego samego wierzchołka, dwóch prostopadłych ścian bocznych, ma miarę 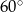60 ∘ . Wiedząc, że objętość tego graniastosłupa jest równa 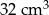32 cm 3 , oblicz pole powierzchni całkowitej tej bryły.

Rozwiązanie

Zaczynamy od rysunku i oznaczmy długość przyprostokątnych trójkąta w podstawie a .

PIC

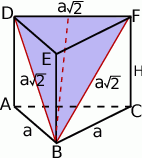
Ponieważ trójkąt w postawie graniastosłupa jest równoramienny, trójkąt 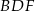BDF też jest równoramienny. Ponadto kąt między jego ramionami jest równy 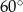60 ∘ , więc trójkąt ten jest równoboczny. W takim razie

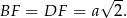
√ -- BF = DF = a 2.

Stosujemy teraz twierdzenie Pitagorasa w trójkącie 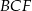BCF .

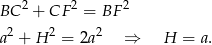
BC 2 + CF 2 = BF 2 2 2 2 a + H = 2a ⇒ H = a.

Zatem objętość graniastosłupa jest równa

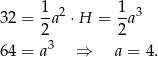
32 = 1a2 ⋅H = 1-a3 2 2 64 = a3 ⇒ a = 4.

Teraz liczymy pole powierzchni.

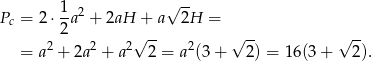
1-2 √ -- Pc = 2⋅ 2a + 2aH + a 2H = 2 2 2√ -- 2 √ -- √ -- = a + 2a + a 2 = a (3 + 2) = 1 6(3+ 2).

 
Odpowiedź: √ -- 2 16(3 + 2) cm

Wersja PDF