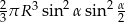/Szkoła średnia/Geometria/Stereometria

Zadanie nr 2849168

Dodaj do ulubionych
Dodaj do rozwiązanych

W kulę o promieniu 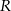R wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem α . Oblicz objętość stożka.

Rozwiązanie

Narysujmy przekrój osiowy opisanej sytuacji.

PIC

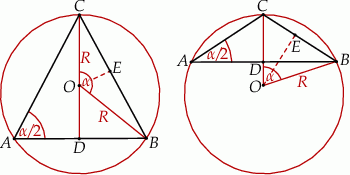
Podana informacja o kącie pod jakim widać tworzącą to po prostu miara kąta 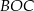BOC . Z twierdzenia o kącie środkowym i wpisanym opartych na tym samym łuku mamy 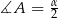∡A = α 2 . Zatem z twierdzenia sinusów

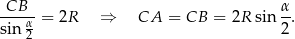
-CB-- α- sin α = 2R ⇒ CA = CB = 2R sin 2 . 2

Długość tworzącej 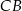CB mogliśmy też wyliczyć z twierdzenia cosinusów w trójkącie 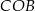COB lub z trójkąta prostokątnego BOE .

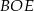Z trójkąta prostokątnego 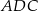ADC mamy

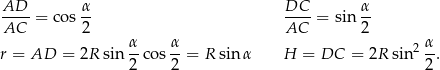
AD-- = cos α- DC--= sin α- AC 2 AC 2 r = AD = 2R sin α-co s α-= R sin α H = DC = 2R sin 2 α-. 2 2 2

Stąd szukana objętość

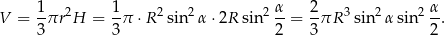
1- 2 1- 2 2 2 α 2- 3 2 2 α- V = 3 πr H = 3π ⋅R sin α⋅ 2R sin 2 = 3 πR sin α sin 2.

 
Odpowiedź: 2 2 2 α 3πR 3sin α sin 2

Wersja PDF