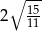Zadanie nr 2891733
W czworościanie 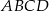 krawędź
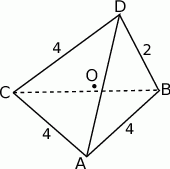
krawędź 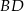 ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
- Oblicz odległość krawędzi
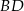 od krawędzi
od krawędzi 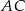 .
. - Wiedząc, że punkt
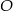 jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka
jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka 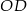 .
.
Rozwiązanie
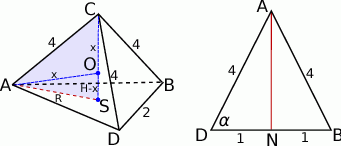
Jedno z tych zadań, gdzie wszystko sprowadza się do wykonania dobrego rysunku.
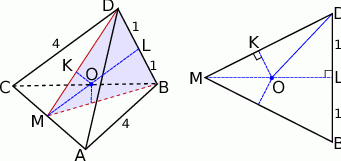
- Aby znaleźć odległość krawędzi
 i
i  musimy znaleźć odcinek, który jest prostopadły do każdej z nich. Na naszym rysunku będzie to odcinek
musimy znaleźć odcinek, który jest prostopadły do każdej z nich. Na naszym rysunku będzie to odcinek  , gdzie
, gdzie 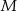 jest środkiem krawędzi
jest środkiem krawędzi 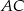 . Jest on wysokością w trójkącie równoramiennym
. Jest on wysokością w trójkącie równoramiennym 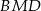 , więc jest prostopadły do
, więc jest prostopadły do 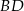 . Ponadto płaszczyzna
. Ponadto płaszczyzna 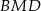 jest prostopadła do
jest prostopadła do 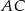 , więc jest on też prostopadły do
, więc jest on też prostopadły do 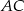 . Długość tego odcinka łatwo wyliczyć z trójkąta prostokątnego
. Długość tego odcinka łatwo wyliczyć z trójkąta prostokątnego 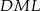 .
. 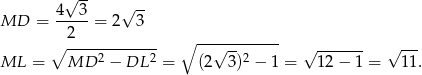
Odpowiedź: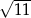
-
Sposób I
Zauważmy, że punkt
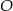 leży w płaszczyźnie
leży w płaszczyźnie 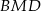 (bo jest równoodległy od wierzchołków
(bo jest równoodległy od wierzchołków 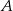 i
i 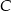 ). Leży on też na prostej
). Leży on też na prostej 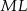 , bo jest równoodległy od
, bo jest równoodległy od 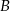 i
i 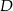 . Ponadto jego rzut
. Ponadto jego rzut 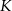 na płaszczyznę
na płaszczyznę 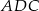 musi być środkiem trójkąta równobocznego
musi być środkiem trójkąta równobocznego 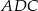 (bo jest równoodległy od wierzchołków
(bo jest równoodległy od wierzchołków 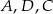 ), czyli
), czyli 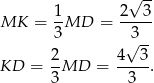
No i zadanie przestało być przestrzenne. Jak popatrzymy na trójkąt równoramienny
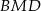 , to znamy długości jego boków oraz odcinka
, to znamy długości jego boków oraz odcinka 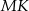 , a mamy wyliczyć
, a mamy wyliczyć 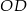 . Możemy tę długość łatwo wyliczyć z trójkąta prostokątnego
. Możemy tę długość łatwo wyliczyć z trójkąta prostokątnego 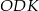 , ale najpierw potrzebujemy znać długość
, ale najpierw potrzebujemy znać długość 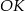 .
. Z podobieństwa trójkątów
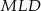 i
i 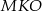 mamy
mamy 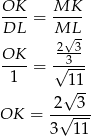
No i pozostało zastosować twierdzenie Pitagorasa w trójkącie
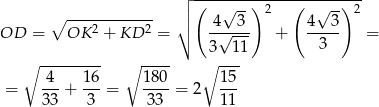
Sposób II
Tym razem obróćmy sobie dany czworościan tak, aby w podstawie był trójkąt równoramienny.
Zauważmy, że punkt
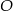 musi leżeć na płaszczyznach prostopadłych do krawędzi
musi leżeć na płaszczyznach prostopadłych do krawędzi  i przechodzących przez ich środki. Ponieważ trójkąty
i przechodzących przez ich środki. Ponieważ trójkąty  i
i 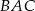 są równoramienne, płaszczyzny te przechodzą przez wierzchołek
są równoramienne, płaszczyzny te przechodzą przez wierzchołek 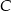 oraz przecinają się wzdłuż wysokości
oraz przecinają się wzdłuż wysokości 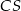 czworościanu. W dodatku spodek
czworościanu. W dodatku spodek 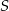 tej wysokości jest środkiem okręgu opisanego na trójkącie
tej wysokości jest środkiem okręgu opisanego na trójkącie 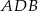 (bo wspomniane płaszczyzny zawierają symetralne boków trójkąta
(bo wspomniane płaszczyzny zawierają symetralne boków trójkąta 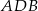 , można też skorzystać z tego, że
, można też skorzystać z tego, że 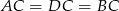 ). W takim razie szukaną odległość
). W takim razie szukaną odległość 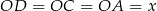 możemy wyliczyć z trójkąta prostokątnego
możemy wyliczyć z trójkąta prostokątnego 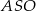 , o ile wyliczymy promień
, o ile wyliczymy promień 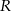 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 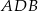 i wysokość
i wysokość 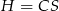 .
. Promień
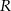 okręgu opisanego na
okręgu opisanego na 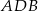 można wyliczyć na różne sposoby, my zastosujemy twierdzenie sinusów. Mamy
można wyliczyć na różne sposoby, my zastosujemy twierdzenie sinusów. Mamy 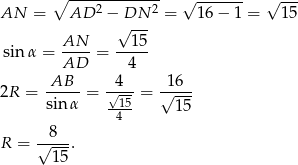
Teraz łatwo możemy wyliczyć wysokość
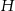 .
. 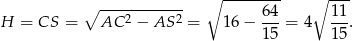
Teraz patrzymy na trójkąt
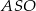
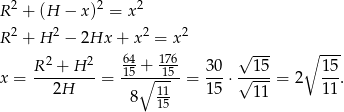
Odpowiedź: