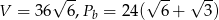/Szkoła średnia/Geometria/Stereometria

Zadanie nr 3053180

Podstawą graniastosłupa jest trójkąt prostokątny równoramienny o ramieniu długości 6. Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 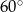60∘ . Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku

PIC

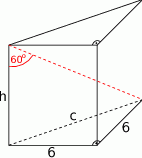
Z twierdzenia Pitagorasa obliczamy długość przeciwprostokątnej c

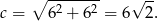
∘ ------- √ -- c = 62 + 62 = 6 2.

Korzystamy z funkcji tangens do obliczenia wysokości graniastosłupa

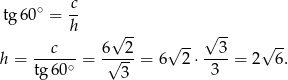
c tg 60∘ = -- h √ -- √ -- --c--- 6--2- √ -- --3- √ -- h = tg60 ∘ = √ 3-= 6 2 ⋅ 3 = 2 6.

Obliczamy objętość graniastosłupa

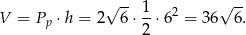
√ -- 1- 2 √ -- V = Pp ⋅h = 2 6⋅ 2 ⋅ 6 = 36 6.

Liczymy pole powierzchni bocznej

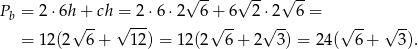
√ -- √ -- √ -- Pb = 2⋅ 6h+ ch = 2 ⋅6⋅ 2 6+ 6 2⋅ 2 6 = √ -- √ --- √ -- √ -- √ -- √ -- = 12(2 6 + 12 ) = 12(2 6 + 2 3) = 24( 6+ 3).

 
Odpowiedź: √ -- √ -- √ -- V = 36 6 ,P = 24( 6 + 3) b

Wersja PDF