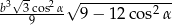Zadanie nr 3080088
Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 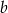 i tworzy z krawędzią podstawy kąt o mierze
i tworzy z krawędzią podstawy kąt o mierze  . Jaką objętość ma ten ostrosłup?
. Jaką objętość ma ten ostrosłup?
Rozwiązanie
Zaczynamy od rysunku.
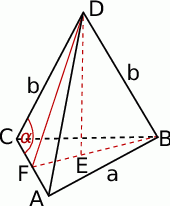
Z trójkąta prostokątnego 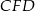 wyliczamy długość
wyliczamy długość  krawędzi podstawy otrosłupa.
krawędzi podstawy otrosłupa.
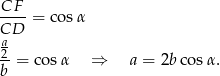
Wysokość ostrosłupa wyliczamy z trójkąta prostokątnego 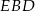 . Aby to zrobić zauważmy, że
. Aby to zrobić zauważmy, że 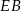 to
to  długości wysokości trójkąta równobocznego
długości wysokości trójkąta równobocznego 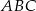 , czyli
, czyli
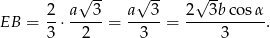
Mamy zatem
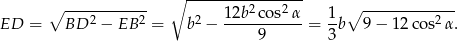
Liczymy teraz objętość (korzystamy ze wzoru na pole trójkąta równobocznego)
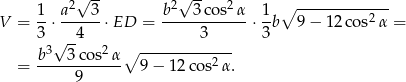
Odpowiedź: