/Szkoła średnia/Geometria/Stereometria

Zadanie nr 3125390

Dodaj do ulubionych
Dodaj do rozwiązanych

Czworościan foremny przecięto płaszczyzną przechodzącą przez krawędź boczną i wysokość podstawy. Jako przekrój otrzymano trójkąt o polu równym 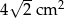√ -- 4 2 cm 2 . Oblicz objętość tego czworościanu.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

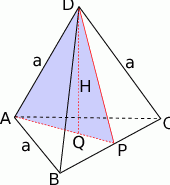
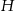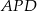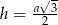Zacznijmy od wyznaczenia wysokości H czworościanu (która jest jednocześnie wysokością trójkąta AP D ). Jeżeli przez a oznaczymy krawędź czworościanu, to korzystając ze wzoru na wysokość w trójkącie równobocznym a√ 3 h = --2- oraz z faktu, że spodek wysokości 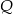Q dzieli wysokość 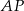AP w stosunku 2:1 mamy

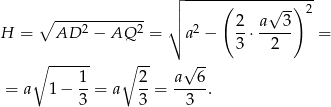
┌ ------------------ ∘ ------------- ││ ( √ -) 2 H = AD 2 − AQ 2 = ∘ a2 − 2⋅ a--3- = 3 2 ∘ ------ ∘ -- √ -- 1- 2- a--6- = a 1 − 3 = a 3 = 3 .

Z podanego pola trójkąta 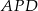AP D mamy

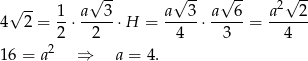
√ -- √ -- √ -- √ -- √ -- 1- a--3- a--3- a--6- a2--2- 4 2 = 2 ⋅ 2 ⋅H = 4 ⋅ 3 = 4 2 16 = a ⇒ a = 4.

Pozostało policzyć objętość czworościanu

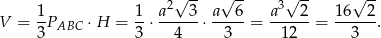
2√ -- √ -- 3√ -- √ -- V = 1P ⋅H = 1-⋅ a---3-⋅ a-6-= a---2-= 16--2. 3 ABC 3 4 3 1 2 3

 
Odpowiedź: √ - 16--2cm 3 3

Wersja PDF