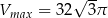Zadanie nr 3134401
Rozpatrujemy wszystkie trójkąty równoramienne o ramionach długości 6. Oblicz cosinus kąta między ramionami tego z tych trójkątów, dla którego objętość bryły powstałej w wyniku obrotu trójkąta dokoła prostej zawierającej jego podstawę jest największa możliwa. Oblicz tę największą objętość.
Rozwiązanie
Szkicujemy opisaną sytuację.
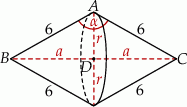
W wyniku opisanego obrotu trójkąta równoramiennego 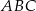 otrzymamy bryłę obrotową składającą się z dwóch stożków o promieniu podstawy
otrzymamy bryłę obrotową składającą się z dwóch stożków o promieniu podstawy  równym wysokości
równym wysokości 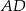 trójkąta
trójkąta 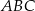 i wysokości
i wysokości  równej połowie podstawy
równej połowie podstawy 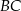 . W szczególności mamy
. W szczególności mamy
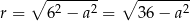
i objętość otrzymanej bryły jest równa
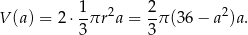
Wyznaczenie bryły o największej objętości sprowadza się więc do wyznaczenia największej wartości funkcji
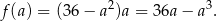
Liczymy pochodną tej funkcji
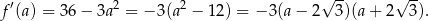
Dziedziną funkcji 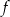 jest przedział
jest przedział 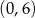 i w tym przedziale pochodna ma jedno miejsce zerowe
i w tym przedziale pochodna ma jedno miejsce zerowe 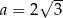 . Ponadto, na lewo od tego miejsca zerowego pochodna jest dodatnia, a na prawo jest ujemna. To oznacza, że funkcja
. Ponadto, na lewo od tego miejsca zerowego pochodna jest dodatnia, a na prawo jest ujemna. To oznacza, że funkcja 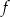 rośnie w przedziale
rośnie w przedziale 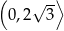 i maleje w przedziale
i maleje w przedziale 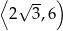 . W takim razie największą objętość bryły otrzymamy dla
. W takim razie największą objętość bryły otrzymamy dla 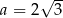 .
.
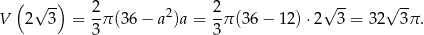
Pozostało obliczyć cosinus kąta między ramionami trójkąta 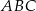 – piszemy twierdzenie cosinusów w tym trójkącie.
– piszemy twierdzenie cosinusów w tym trójkącie.
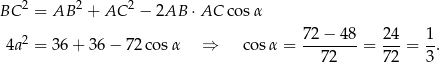
Odpowiedź: 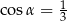 ,
,