Zadanie nr 3135936
Punkty 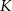 i
i 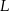 są środkami krawędzi
są środkami krawędzi 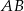 i
i 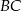 sześcianu
sześcianu 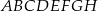 o krawędzi długości 1. Punkt
o krawędzi długości 1. Punkt 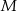 jest środkiem ściany
jest środkiem ściany 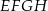 (zobacz rysunek). Oblicz pole trójkąta
(zobacz rysunek). Oblicz pole trójkąta 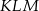 .
.
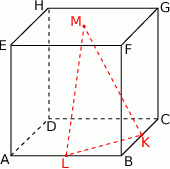
Rozwiązanie
Niech 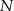 będzie środkiem ściany
będzie środkiem ściany 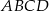 , a
, a 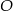 niech będzie środkiem odcinka
niech będzie środkiem odcinka 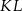 .
.
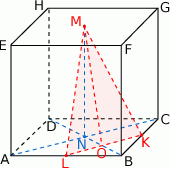
Podstawa trójkąta równoramiennego 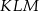 ma długość równą połowie przekątnej kwadratu w podstawie, czyli
ma długość równą połowie przekątnej kwadratu w podstawie, czyli

Długość wysokość 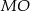 tego trójkąta możemy obliczyć z trójkąta prostokątnego
tego trójkąta możemy obliczyć z trójkąta prostokątnego 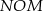 – aby to zrobić zauważmy, że
– aby to zrobić zauważmy, że
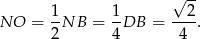
Obliczamy długość odcinka 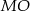 .
.
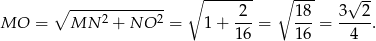
Pozostało obliczyć pole trójkąta 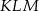 .
.
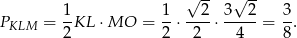
Odpowiedź: 

