/Szkoła średnia/Geometria/Stereometria

Zadanie nr 3142887

Dodaj do ulubionych
Dodaj do rozwiązanych

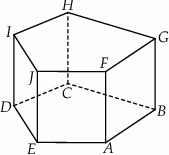
Dany jest graniastosłup prosty o podstawie pięciokątnej 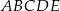ABCDE (zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu dwa razy mniejszym niż pole pięciokąta 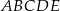ABCDE . Pole powierzchni całkowitej tego graniastosłupa jest równe 153. Oblicz jego objętość.

PIC

Rozwiązanie

Korzystamy najpierw z podanej informacji o polu powierzchni całkowitej graniastosłupa

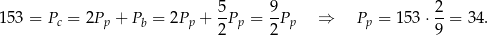
15 3 = Pc = 2Pp + Pb = 2Pp + 5-Pp = 9Pp ⇒ Pp = 153 ⋅ 2-= 34. 2 2 9

Jeżeli teraz oznaczymy przez a długość krawędzi graniastosłupa (którejkolwiek, bo wszystkie mają tę samą długość), to

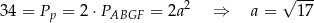
--- 3 4 = P = 2 ⋅P = 2a2 ⇒ a = √ 17 p ABGF

i objętość graniastosłupa jest równa

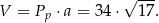
√ --- V = Pp ⋅a = 34 ⋅ 17.

 
Odpowiedź: √ --- V = 34 1 7

Wersja PDF