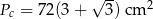/Szkoła średnia/Geometria/Stereometria

Zadanie nr 3261859

Dodaj do ulubionych
Dodaj do rozwiązanych

Ściany boczne ostrosłupa prawidłowego trójkątnego są trójkątami o przyprostokątnych długości 12 cm. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

Rozwiązanie

Zaczynamy od schematycznego rysunku.

PIC

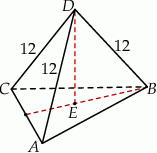
Ponieważ ściany są trójkątami prostokątnymi, łatwo jest obliczyć długość krawędzi podstawy

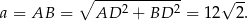
∘ ------------ √ -- a = AB = AD 2 + BD 2 = 12 2.

Długość odcinka 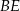BE to 23 wysokości trójkąta równobocznego w podstawie, czyli

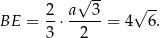
√ -- 2 a 3 √ -- BE = --⋅----- = 4 6. 3 2

Teraz łatwo obliczyć wysokość ostrosłupa

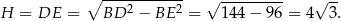
∘ ------------ H = DE = BD 2 − BE 2 = √ 144-−-96-= 4√ 3.

Pole podstawy ostrosłupa jest równe

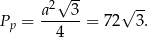
√ -- a2 3 √ -- Pp = ------= 72 3 . 4

Liczymy objętość ostrosłupa

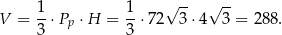
1 1 √ -- √ -- V = -⋅ Pp ⋅ H = --⋅72 3 ⋅4 3 = 288. 3 3

Pole ściany bocznej ostrosłupa jest równe

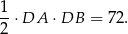
1 2-⋅DA ⋅ DB = 72.

Zatem pole powierzchni całkowitej ostrosłupa jest równe

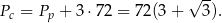
√ -- P = P + 3 ⋅72 = 72 (3+ 3). c p

 
Odpowiedź: 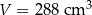3 V = 288 cm , √ -- 2 Pc = 72(3+ 3) cm

Wersja PDF