/Szkoła średnia/Geometria/Stereometria

Zadanie nr 3404653

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 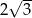√ -- 2 3 . Oblicz objętość tego ostrosłupa jeżeli ściana boczna jest nachylona do podstawy pod kątem 45 ∘ .

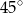Rozwiązanie

Zaczynamy od schematycznego rysunku.

PIC

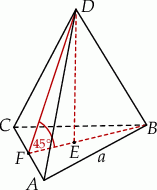
Wysokość ostrosłupa wyliczymy z trójkąta prostokątnego 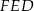FED , ale najpierw musimy wyliczyć długość odcinka 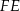FE . Jest on równy 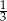13 wysokości trójkąta 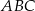ABC (w ten sposób środek trójkąta równobocznego dzieli wysokość), czyli

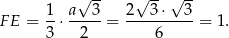
-- -- -- 1 a√ 3 2√ 3⋅√ 3 F E = --⋅ -----= ----------= 1. 3 2 6

Liczymy teraz wysokość ostrosłupa:

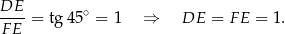
DE ∘ ---- = tg 45 = 1 ⇒ DE = FE = 1. FE

Zatem objętość ostrosłupa jest równa (korzystamy ze wzoru na pole trójkąta równobocznego).

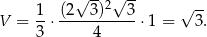
1 (2√ 3)2√ 3- √ -- V = --⋅-----------⋅1 = 3. 3 4

 
Odpowiedź: √ -- 3

Wersja PDF