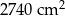/Szkoła średnia/Geometria/Stereometria

Zadanie nr 3612925

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą graniastosłupa jest trapez równoramienny o podstawach długości 56 cm i 40 cm oraz wysokości 15 cm. Wiedząc, że wysokość graniastosłupa jest równa 10 cm, oblicz jego pole powierzchni całkowitej.

Rozwiązanie

Możemy zacząć od szkicowego rysunku.

PIC

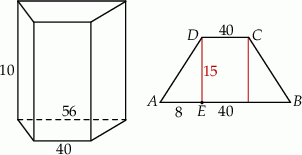
Zacznijmy od wyliczenia długości ramion trapezu. Ponieważ trapez jest równoramienny

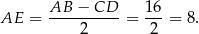
AE = AB--−-CD--= 16-= 8. 2 2

Zatem z trójkąta prostokątnego 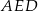AED mamy

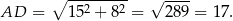
∘ --------- √ ---- AD = 152 + 82 = 289 = 17.

Pole trapezu jest równe

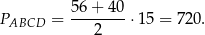
PABCD = 56+--40-⋅15 = 72 0. 2

Aby otrzymać pole powierzchni całkowitej graniastosłupa, trzeba wziąć dwa pola trapezu i pola czterech prostokątów, czyli

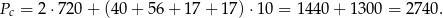
Pc = 2⋅7 20+ (40+ 56+ 17 + 17) ⋅10 = 14 40+ 1300 = 2 740.

 
Odpowiedź: 2 274 0 cm

Wersja PDF