/Szkoła średnia/Geometria/Stereometria

Zadanie nr 3791774

Objętość graniastosłupa prawidłowego trójkątnego jest równa 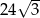√ -- 24 3 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.

Wersja PDF

Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

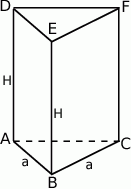
Liczymy

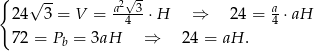
{ √ -- 2√- 24 3 = V = a-43 ⋅H ⇒ 24 = a4 ⋅aH 72 = P = 3aH ⇒ 2 4 = aH . b

Podstawiając 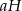aH z drugiego równania do pierwszego mamy

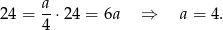
a- 24 = 4 ⋅2 4 = 6a ⇒ a = 4.

Zatem 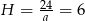H = 24 = 6 a .  
Odpowiedź: Krawędź podstawy: 4, wysokość: 6.

Wersja PDF