/Szkoła średnia/Geometria/Stereometria

Zadanie nr 3945912

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz objętość ostrosłupa prawidłowego trójkątnego o krawędzi podstawy 6 cm i krawędzi bocznej 12 cm.

Rozwiązanie

Zaczynamy od schematycznego rysunku.

PIC

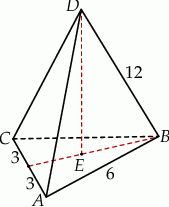
Wysokość trójkąta równobocznego w podstawie jest równa

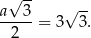
√ -- a--3-= 3 √ 3. 2

Długość odcinka 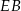EB to dokładnie 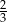23 wysokości (bo tak dzieli wysokość środek trójkąta równobocznego), czyli

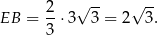
EB = 2-⋅3 √ 3 = 2√ 3. 3

Teraz, stosując twierdzenie Pitagorasa w trójkącie 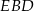EBD , mamy

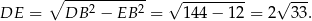
∘ ------------ √ --------- √ --- DE = DB 2 − EB 2 = 144 − 12 = 2 33.

Zatem objętość jest równa (korzystamy ze wzoru na pole trójkąta równobocznego)

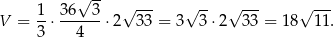
√ -- 1- 36---3 √ --- √ -- √ --- √ --- V = 3 ⋅ 4 ⋅ 2 33 = 3 3 ⋅2 3 3 = 18 11.

 
Odpowiedź: √ --- 3 18 1 1 cm

Wersja PDF