/Szkoła średnia/Geometria/Stereometria

Zadanie nr 4015161

Dodaj do ulubionych
Dodaj do rozwiązanych

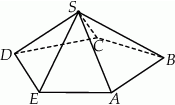
Dany jest ostrosłup o podstawie pięciokątnej 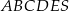ABCDES (zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta 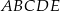ABCDE . Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.

PIC

Rozwiązanie

Jeżeli oznaczymy przez 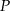P pole podstawy ostrosłupa, to każda ze ścian bocznych ma pole 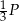13P i z podanego pola powierzchni całkowitej mamy

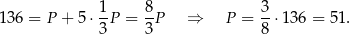
136 = P + 5⋅ 1P = 8P ⇒ P = 3-⋅136 = 5 1. 3 3 8

 
Odpowiedź: 51

Wersja PDF