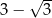Zadanie nr 4190056
W sześcian o krawędzi 4 wpisano kulę styczną do trzech ścian sześcianu oraz przechodzącą przez środek sześcianu. Oblicz promień tej kuli.
Rozwiązanie
Zaczynamy oczywiście od rysunku. Niech 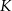 będzie środkiem, a
będzie środkiem, a  promieniem kuli, o której mowa w treści zadania,
promieniem kuli, o której mowa w treści zadania, 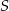 niech będzie środkiem sześcianu.
niech będzie środkiem sześcianu.
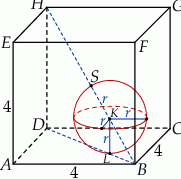
Po pierwsze zauważmy, że środek kuli, o której mowa w treści zadania leży na przekątnej 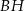 sześcianu. Tak jest, bo przekątna ta składa się punktów, które są w tej samej odległości od ścian
sześcianu. Tak jest, bo przekątna ta składa się punktów, które są w tej samej odległości od ścian 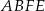 ,
, 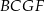 i
i 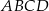 . Jeżeli
. Jeżeli 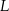 jest punktem styczności kuli ze ścianą
jest punktem styczności kuli ze ścianą 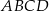 , to
, to
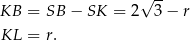
Korzystamy teraz z podobieństwa trójkątów 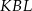 i
i  .
.
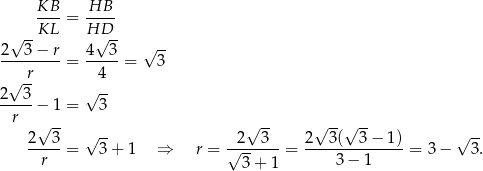
Odpowiedź: