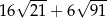/Szkoła średnia/Geometria/Stereometria

Zadanie nr 4372303

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa jest prostokąt, którego stosunek długości boków wynosi 4:3. Pole podstawy ostrosłupa jest równe 48. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 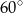6 0∘ . Oblicz pole powierzchni bocznej tego ostrosłupa.

Rozwiązanie

Szkicujemy ostrosłup

PIC

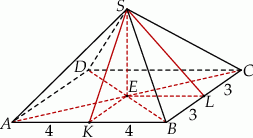
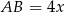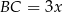Jeżeli oznaczymy AB = 4x i BC = 3x , to z podanego pola podstawy mamy

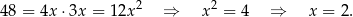
48 = 4x ⋅3x = 12x2 ⇒ x 2 = 4 ⇒ x = 2.

Wysokość ostrosłupa obliczymy z trójkąta prostokątnego 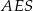AES , ale zanim to zrobimy, obliczmy długość odcinka AE .

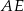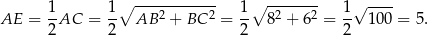
------------ ------- 1- 1-∘ 2 2 1∘ 2 2 1√ ---- AE = 2 AC = 2 AB + BC = 2 8 + 6 = 2 100 = 5.

Obliczamy teraz z trójkąta 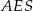AES wysokość ostrosłupa.

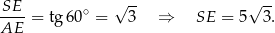
SE ∘ √ -- √ -- AE--= tg60 = 3 ⇒ SE = 5 3.

Liczymy jeszcze wysokości ścian bocznych

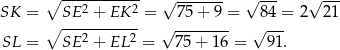
∘ ----------- √ ------- √ --- √ --- SK = SE 2 + EK 2 = 75 + 9 = 8 4 = 2 21 ∘ ----------- √ -------- √ --- SL = SE 2 + EL 2 = 75+ 16 = 91 .

Pole powierzchni bocznej jest więc równe

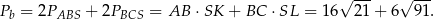
√ --- √ --- Pb = 2PABS + 2PBCS = AB ⋅SK + BC ⋅ SL = 1 6 21 + 6 91.

 
Odpowiedź: √ --- √ --- 16 2 1+ 6 91

Wersja PDF