/Szkoła średnia/Geometria/Stereometria

Zadanie nr 4375644

Dodaj do ulubionych
Dodaj do rozwiązanych

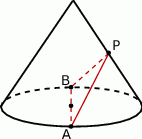
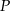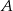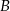Środek P tworzącej stożka połączono z końcami A i B średnicy koła w podstawie stożka tak, że 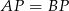AP = BP . Wiedząc, że kąt rozwarcia stożka jest równy 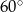6 0∘ , oblicz kąty trójkąta ABP .

PIC

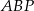Rozwiązanie

Kluczowe w tym zadaniu jest zauważanie, że wysokość 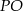P O trójkąta 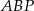ABP jest równa promieniowi podstawy stożka.

PIC

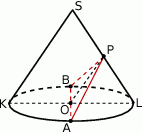
Można to zrobić na różne sposoby, np. 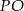PO łączy środki boków w trójkącie 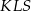KLS , więc 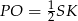P O = 12SK , ale z założenia trójkąt 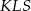KLS jest równoboczny (bo jest równoramienny z kątem 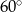60∘ ), zatem

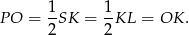
1- 1- PO = 2SK = 2 KL = OK .

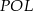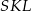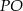Inny sposób, to popatrzeć na trójkąt POL . Jest on podobny do trójkąta SKL (bo P O łączy środki boków w 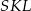SKL ), więc też jest równoboczny. Zatem P O = OL .

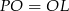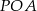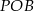Tak czy inaczej, trójkąty P OA i P OB są prostokątne i równoramienne, czyli

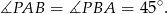
∡PAB = ∡P BA = 45∘.

Stąd 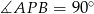∡AP B = 90∘ .  
Odpowiedź: ∡PAB = ∡P BA = 45∘ , ∡AP B = 90∘

Wersja PDF