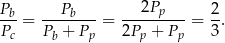Zadanie nr 4439979
W ostrosłupie prawidłowym trójkątnym 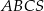 cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy
cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy 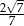 . Wykaż, że pole powierzchni bocznej tego ostrosłupa stanowi
. Wykaż, że pole powierzchni bocznej tego ostrosłupa stanowi  jego pola powierzchni całkowitej.
jego pola powierzchni całkowitej.
Rozwiązanie
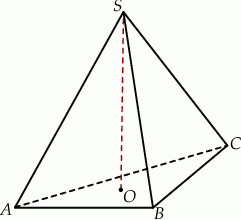
Oznaczmy przez  krawędź podstawy, a przez
krawędź podstawy, a przez 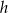 i
i 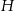 odpowiednio długości wysokości ściany bocznej oraz wysokości ostrosłupa.
odpowiednio długości wysokości ściany bocznej oraz wysokości ostrosłupa.
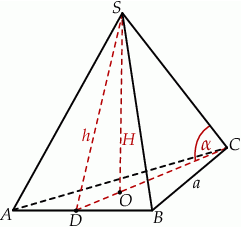
Ponieważ środek 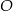 trójkąta równobocznego
trójkąta równobocznego 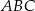 dzieli jego wysokość
dzieli jego wysokość 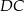 w stosunku 2:1, mamy
w stosunku 2:1, mamy
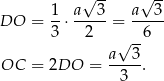
Z podanego 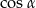 obliczmy
obliczmy 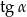 .
.
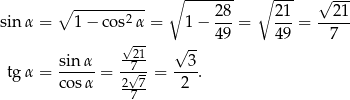
Stąd
Teraz z trójkąta prostokątnego 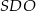 obliczamy długość
obliczamy długość 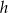 wysokości ściany bocznej.
wysokości ściany bocznej.
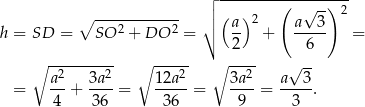
W takim razie
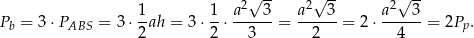
Stąd