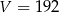/Szkoła średnia/Geometria/Stereometria

Zadanie nr 4577591

Dodaj do ulubionych
Dodaj do rozwiązanych

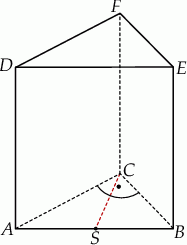
Podstawą graniastosłupa prostego 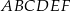ABCDEF jest trójkąt prostokątny 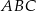ABC , w którym 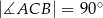|∡ACB | = 9 0∘ (zobacz rysunek). Stosunek długości przyprostokątnej 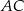AC tego trójkąta do długości przyprostokątnej 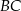BC jest równy 4:3. Punkt 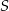S jest środkiem okręgu opisanego na trójkącie 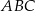ABC , a długość odcinka 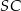SC jest równa 5. Pole ściany bocznej 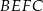BEF C graniastosłupa jest równe 48. Oblicz objętość tego graniastosłupa.

PIC

Rozwiązanie

Środek okręgu opisanego na trójkącie prostokątnym to dokładnie środek przeciwprostokątnej (przyprostokątna jest średnicą tego okręgu). Zatem

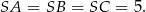
SA = SB = SC = 5.

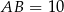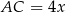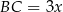Stąd AB = 1 0 . Jeżeli teraz oznaczymy AC = 4x i BC = 3x , to na mocy twierdzenia Pitagorasa mamy

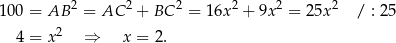
2 2 2 2 2 2 100 = AB = AC + BC = 16x + 9x = 25x / : 25 4 = x2 ⇒ x = 2.

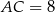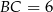Mamy stąd AC = 8 i BC = 6 . Wykorzystujemy teraz informację o polu ściany BEF C .

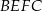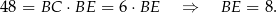
48 = BC ⋅BE = 6 ⋅BE ⇒ BE = 8.

Objętość graniastosłupa jest więc równa

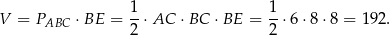
1 1 V = PABC ⋅ BE = --⋅AC ⋅BC ⋅BE = --⋅6 ⋅8⋅ 8 = 192. 2 2

 
Odpowiedź: V = 192

Wersja PDF