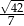/Szkoła średnia/Geometria/Stereometria

Zadanie nr 4587520

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym czworokątnym 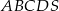ABCDS o podstawie 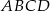ABCD i wierzchołku 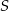S trójkąt 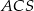ACS jest równoboczny i ma bok długości 8. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek).

PIC

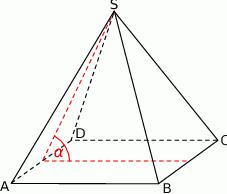
Rozwiązanie

Oznaczmy długość krawędzi podstawy ostrosłupa przez a .

PIC

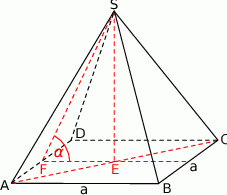
Z podanych informacji wiemy, że przekątna kwadratu w podstawie ma długość

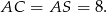
AC = AS = 8.

Zatem

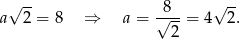
√ -- √ -- a 2 = 8 ⇒ a = √8--= 4 2. 2

Ze wzoru na wysokość trójkąta równobocznego obliczamy długość wysokości ostrosłupa

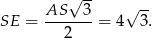
√ -- AS 3 √ -- SE = -------= 4 3. 2

Obliczamy teraz długość przeciwprostokątnej SF trójkąta SF E .

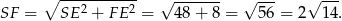
∘ ----------- ------- --- √ --- SF = SE 2 + F E2 = √ 4 8+ 8 = √ 56 = 2 14.

Stąd

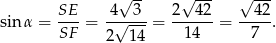
√ -- √ --- √ --- sinα = SE- = 4√-3--= 2--42-= --42. SF 2 14 14 7

 
Odpowiedź: √ -- --42 7

Wersja PDF