Zadanie nr 4634665
W ostrosłupie prawidłowym czworokątnym przeciwległe krawędzie boczne są prostopadłe, a wysokość ściany bocznej poprowadzona z wierzchołka ostrosłupa ma długość 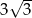 . Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
Rozwiązanie
Zacznijmy od rysunku i oznaczmy krawędź podstawy przez 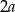 (
(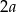 a nie
a nie  , żeby nie mieć ułamków).
, żeby nie mieć ułamków).
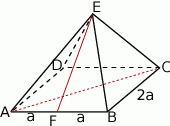
Rozpoczniemy od wyliczenia (na dwa sposoby)  .
.
Sposób I
Z trójkąta prostokątnego 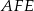 wyliczamy
wyliczamy 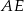 ,
,
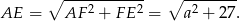
Ponieważ trójkąt 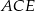 jest równoramienny i prostokątny, jest to połówka kwadratu, zatem
jest równoramienny i prostokątny, jest to połówka kwadratu, zatem
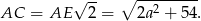
Z drugiej strony, ponieważ w podstawie ostrosłupa jest kwadrat o boku 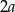 , mamy
, mamy
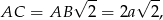
co daje nam równanie
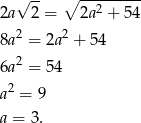
Sposób II
Zauważmy, że trójkąty 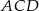 i
i 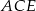 są oba równoramienne i prostokątne. Ponieważ mają wspólną przeciwprostokątną muszą być przystające. Zatem
są oba równoramienne i prostokątne. Ponieważ mają wspólną przeciwprostokątną muszą być przystające. Zatem 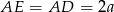 i trójkąty w ścianach bocznych są równoboczne. Ze wzoru na wysokość w trójkącie równobocznym mamy równanie
i trójkąty w ścianach bocznych są równoboczne. Ze wzoru na wysokość w trójkącie równobocznym mamy równanie
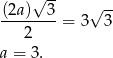
Przechodzimy teraz do obliczania objętości i pola powierzchni.
Jak już zauważyliśmy, trójkąt 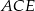 to połówka kwadratu, zatem jego wysokość
to połówka kwadratu, zatem jego wysokość 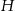 opuszczona z wierzchołka
opuszczona z wierzchołka 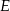 (czyli wysokość ostrosłupa) to dokładnie połowa odcinka
(czyli wysokość ostrosłupa) to dokładnie połowa odcinka 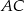 , czyli
, czyli
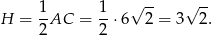
Liczymy teraz objętość ostrosłupa
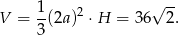
Liczymy teraz pole powierzchni całkowitej
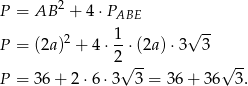
Odpowiedź: Objętość: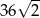 , pole powierzchni:
, pole powierzchni: