Zadanie nr 4724176
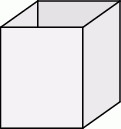
Zakład produkcyjny planuje wytwarzanie pojemników o objętości 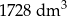 , które mają kształt otwartego graniastosłupa prawidłowego czworokątnego (bez górnej podstawy – zobacz rysunek).
, które mają kształt otwartego graniastosłupa prawidłowego czworokątnego (bez górnej podstawy – zobacz rysunek).
Koszt produkcji 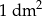 podstawy tego pojemnika wynosi 0,3 zł, a koszt produkcji
podstawy tego pojemnika wynosi 0,3 zł, a koszt produkcji 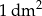 jego ścian bocznych wynosi 0,2 zł. Ponadto, do kosztu produkcji należy doliczyć niezbędne wzmocnienie krawędzi podstawy w cenie 4,2 zł za 1 dm długości. Oblicz jakie powinny być wymiary tego pojemnika tak, aby koszt jego produkcji był najmniejszy możliwy.
jego ścian bocznych wynosi 0,2 zł. Ponadto, do kosztu produkcji należy doliczyć niezbędne wzmocnienie krawędzi podstawy w cenie 4,2 zł za 1 dm długości. Oblicz jakie powinny być wymiary tego pojemnika tak, aby koszt jego produkcji był najmniejszy możliwy.
Rozwiązanie
Oznaczmy przez  długość krawędzi podstawy, a przez
długość krawędzi podstawy, a przez 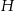 wysokość prostopadłościanu. Z podanej objętości mamy więc
wysokość prostopadłościanu. Z podanej objętości mamy więc
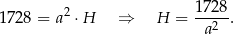
Liczymy teraz koszt wyprodukowania pojemnika
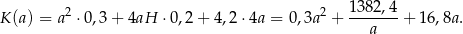
Dziedziną tej funkcji jest przedział 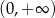 . Interesuje nas jej wartość najmniejsza, więc liczymy pochodną
. Interesuje nas jej wartość najmniejsza, więc liczymy pochodną
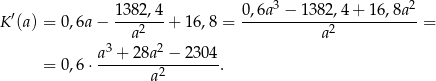
Teraz jest trochę zabawy – musimy znaleźć przynajmniej jeden pierwiastek licznika – sprawdzamy dzielniki wyrazu wolnego 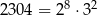 . Najmniejszy z pierwiastków dodatnich to
. Najmniejszy z pierwiastków dodatnich to 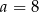 . Dzielimy teraz wielomian w liczniku przez
. Dzielimy teraz wielomian w liczniku przez 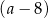 – my zrobimy to grupując wyrazy.
– my zrobimy to grupując wyrazy.
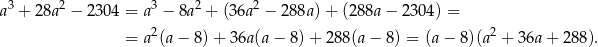
Rozkładamy jeszcze trójmian w nawiasie.
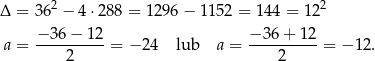
Pochodna jest więc równa
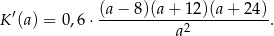
To oznacza, że pochodna jest ujemna dla 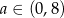 i dodatnia dla
i dodatnia dla 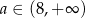 . Funkcja
. Funkcja 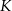 jest więc malejąca dla
jest więc malejąca dla 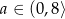 i rosnąca dla
i rosnąca dla 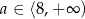 . Najmniejszy koszt pojemnika otrzymamy więc dla
. Najmniejszy koszt pojemnika otrzymamy więc dla 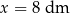 . Wysokość graniastosłupa jest wtedy równa
. Wysokość graniastosłupa jest wtedy równa
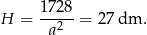
Odpowiedź: