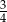/Szkoła średnia/Geometria/Stereometria

Zadanie nr 4724275

Dodaj do ulubionych
Dodaj do rozwiązanych

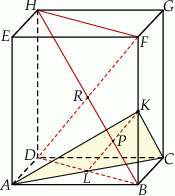
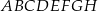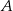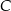Dany jest prostopadłościan ABCDEF GH . Przez wierzchołki A i C oraz środek 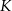K krawędzi 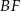BF poprowadzono płaszczyznę, która przecina przekątną 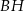BH w punkcie 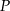P (zobacz rysunek).

PIC

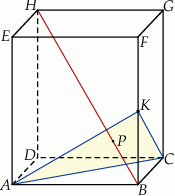
Oblicz 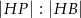|HP | : |HB | .

Rozwiązanie

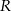Niech L będzie środkiem ściany ABCD , a R środkiem prostopadłościanu.

PIC

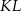Odcinek KL łączy środki boków w trójkącie 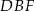DBF , więc trójkąt 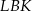LBK jest podobny do trójkąta 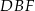DBF w skali 1:2. Stąd

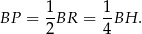
BP = 1BR = 1-BH . 2 4

To oznacza, że

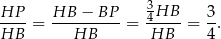
3 HP-- HB--−-BP-- 4HB-- 3- HB = HB = HB = 4 .

 
Odpowiedź: 3 4

Wersja PDF