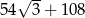Zadanie nr 4745486
Podstawą graniastosłupa 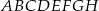 o objętości 162 jest prostokąt
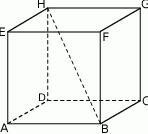
o objętości 162 jest prostokąt 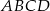 (zobacz rysunek), którego przekątna tworzy z jego bokiem kąt
(zobacz rysunek), którego przekątna tworzy z jego bokiem kąt 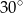 . Przekątna
. Przekątna 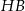 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 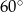 stopni. Oblicz pole powierzchni całkowitej tego graniastosłupa.
stopni. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Rozwiązanie
Oznaczmy przez 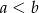 boki prostokąta w podstawie.
boki prostokąta w podstawie.
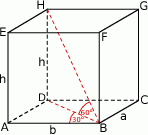
Z trójkąta prostokątnego 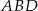 mamy
mamy
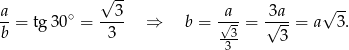
Obliczmy jeszcze długość przekątnej podstawy
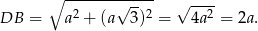
Z trójkąta prostokątnego 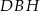 obliczamy długość wysokości graniastosłupa.
obliczamy długość wysokości graniastosłupa.
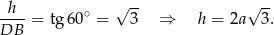
Korzystamy teraz z podanej informacji o objętości graniastosłupa.
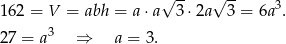
Zatem
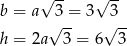
i pole powierzchni całkowitej jest równe
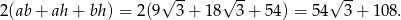
Odpowiedź: