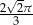/Szkoła średnia/Geometria/Stereometria

Zadanie nr 4771554

Dodaj do ulubionych
Dodaj do rozwiązanych

Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest wycinkiem koła o promieniu 3 i kącie środkowym 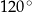120∘ (zobacz rysunek). Oblicz objętość tego stożka.

ZINFO-FIGURE

Rozwiązanie

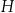Aby obliczyć objętość stożka, potrzebujemy promień podstawy r i wysokość H . Zauważmy, że długość łuku podanego wycinka kołowego, to dokładnie długość okręgu w podstawie stożka. Pozwoli nam to obliczyć promień podstawy:

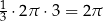  • długość łuku odcinka kołowego: 1⋅ 2π ⋅3 = 2 π 3 ,

  • długość okręgu w podstawie: 2πr .

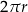Mamy zatem 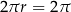2πr = 2π , czyli 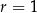r = 1 (mogliśmy też obliczyć r , korzystając ze wzoru na pole powierzchni bocznej stożka).

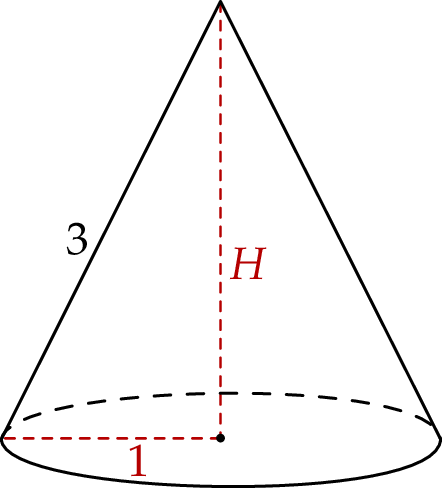
ZINFO-FIGURE

Pozostało obliczyć 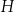H . Stosujemy twierdzenie Pitagorasa:

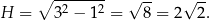
∘ ------- -- -- H = 32 − 12 = √ 8 = 2√ 2.

Korzystamy teraz ze wzoru na objętość:

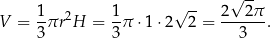
√ -- 1- 2 1- √ -- 2--2π- V = 3 πr H = 3π ⋅1 ⋅2 2 = 3 .

 
Odpowiedź: √ - 2--2π 3

Wersja PDF