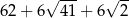/Szkoła średnia/Geometria/Stereometria

Zadanie nr 4844968

Dodaj do ulubionych
Dodaj do rozwiązanych

Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.

PIC

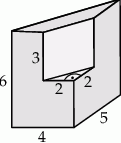
Rozwiązanie

Obliczmy najpierw objętość dużego graniastosłupa.

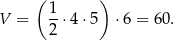
( 1 ) V = --⋅4⋅5 ⋅6 = 60 . 2

Zanim obliczymy pole powierzchni, obliczmy długość przeciwprostokątnej trójkąta w podstawie.

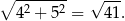
∘ ------- √ --- 42 + 5 2 = 41.

Zatem pole powierzchni jest równe

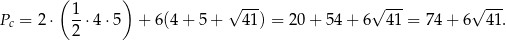
( ) --- --- --- P = 2 ⋅ 1-⋅4 ⋅5 + 6 (4+ 5+ √ 41) = 20 + 54 + 6√ 41 = 74+ 6√ 41. c 2

Obliczmy objętość wyciętej bryły

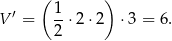
( 1 ) V ′ = -⋅ 2⋅2 ⋅3 = 6. 2

Zatem objętość bryły po wycięciu jest równa

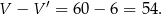
′ V − V = 60 − 6 = 54 .

Pole powierzchni uległo następującej zmianie: wycięto dwa prostokąty o bokach 2 i 3 oraz trójkąt prostokątny, a dodano prostokąt o bokach 3 i 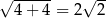√ ------ √ -- 4 + 4 = 2 2 oraz taki sam trójkąt jak wycięty. Zatem pole powierzchni zmienia się o

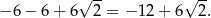
√ -- √ -- − 6 − 6 + 6 2 = − 12+ 6 2.

Zatem jest równe:

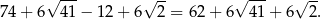
√ --- √ -- √ --- √ -- 74 + 6 41 − 12 + 6 2 = 62 + 6 41 + 6 2.

 
Odpowiedź: Objętość: 54, pole powierzchni: √ --- √ -- 62 + 6 41+ 6 2

Wersja PDF