Zadanie nr 4926794
Czworościan foremny przecięto płaszczyzną 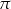 styczną do kuli wpisanej w ten czworościan (tzn. kuli stycznej do wszystkich ścian czworościanu) oraz równoległą do jednej ze ścian czworościanu. Oblicz stosunek objętości brył, na które płaszczyzna
styczną do kuli wpisanej w ten czworościan (tzn. kuli stycznej do wszystkich ścian czworościanu) oraz równoległą do jednej ze ścian czworościanu. Oblicz stosunek objętości brył, na które płaszczyzna 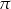 podzieliła czworościan.
podzieliła czworościan.
Rozwiązanie
Próbujemy naszkicować opisaną sytuację. Niech 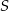 będzie środkiem kuli wpisanej w czworościan, a
będzie środkiem kuli wpisanej w czworościan, a 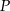 punktem wspólnym płaszczyzny
punktem wspólnym płaszczyzny 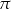 i wysokości
i wysokości 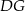 czworościanu.
czworościanu.
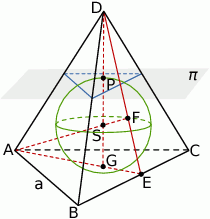
Rozpocznijmy od obliczenia długości wysokości 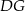 czworościanu oraz promienia
czworościanu oraz promienia 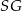 kuli wpisanej w ten czworościan.
kuli wpisanej w ten czworościan.
Przyprostokątna 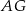 trójkąta prostokątnego
trójkąta prostokątnego 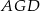 to
to 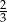 wysokości
wysokości 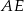 trójkąta równobocznego
trójkąta równobocznego 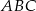 , więc
, więc
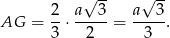
Stąd
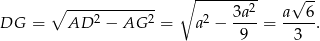
Korzystamy teraz z podobieństwa trójkątów prostokątnych 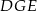 i
i 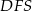 .
.
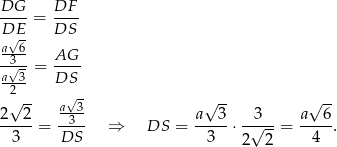
Stąd
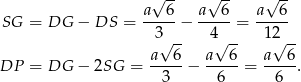
To oznacza, że czworościan odcięty płaszczyzną 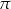 jest podobny do całego czworościanu w skali
jest podobny do całego czworościanu w skali
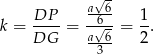
Jego objętość 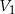 stanowi więc
stanowi więc 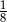 objętości
objętości 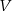 dużego czworościanu. Interesujący nas stosunek objętości jest więc równy
dużego czworościanu. Interesujący nas stosunek objętości jest więc równy
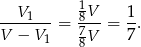
Odpowiedź: