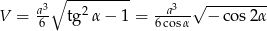Zadanie nr 4938334
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość  . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę
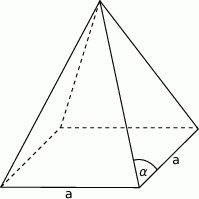
. Kąt między krawędzią boczną, a krawędzią podstawy ma miarę 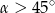 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
(zobacz rysunek). Oblicz objętość tego ostrosłupa.
Rozwiązanie
Dorysujmy wysokość ostrosłupa oraz wysokość ściany bocznej.
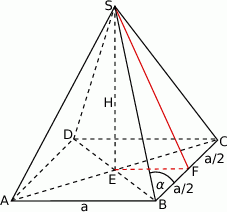
Ponieważ znamy długość krawędzi podstawy, wystarczy obliczyć wysokość 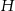 ostrosłupa.
ostrosłupa.
Sposób I
Najpierw z trójkąta 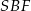 obliczamy wysokość ściany bocznej.
obliczamy wysokość ściany bocznej.
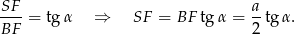
Teraz korzystamy z twierdzenia Pitagorasa w trójkącie 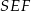 .
.
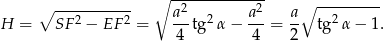
W takim razie objętość ostrosłupa jest równa
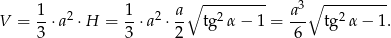
Sposób II
Tym razem obliczymy najpierw długość krawędzi bocznej ostrosłupa.
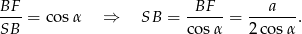
Teraz korzystamy z twierdzenia Pitagorasa w trójkącie 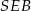 .
.
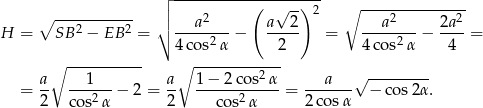
W powyższym przekształceniu korzystaliśmy z tego, że 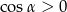 i
i 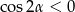 . Liczymy teraz objętość ostrosłupa.
. Liczymy teraz objętość ostrosłupa.
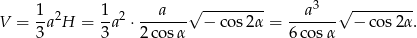
Odpowiedź: