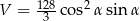/Szkoła średnia/Geometria/Stereometria

Zadanie nr 4996197

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość 4 cm i jest nachylona do płaszczyzny podstawy pod kątem α . Oblicz objętość ostrosłupa.

Rozwiązanie

Zacznijmy od rysunku.

PIC

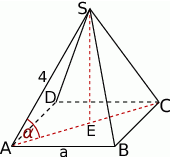
Z trójkąta prostokątnego 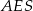AES wyliczamy wysokość 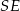SE ostrosłupa oraz odcinek AE .

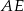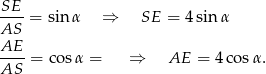
SE--= sin α ⇒ SE = 4 sin α AS AE ----= cosα = ⇒ AE = 4 cosα . AS

Ponieważ w podstawie jest kwadrat, mamy

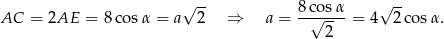
√ -- 8-cos-α √ -- AC = 2AE = 8co sα = a 2 ⇒ a = √ 2- = 4 2 cosα .

Liczymy teraz objętość ostrosłupa.

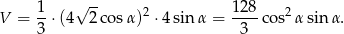
√ -- V = 1⋅ (4 2cos α)2 ⋅ 4sinα = 128-cos2 αsin α. 3 3

 
Odpowiedź: V = 1238 cos2α sin α

Wersja PDF