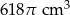Zadanie nr 5061369
Trapez równoramienny o podstawach długości 14 cm i 26 cm oraz o wysokości 6 cm obraca się wokół swojej osi symetrii. Oblicz objętość otrzymanej bryły.
Rozwiązanie
Zaczynamy od rysunku – od razu rysujemy przekrój osiowy otrzymanej sytuacji.
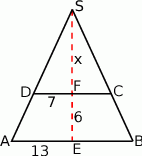
Widać, że otrzymamy ścięty stożek, więc możemy policzyć jego objętość odejmując od objętości stożka o przekroju 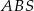 objętość stożka o przekroju
objętość stożka o przekroju 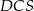 . Znamy promienie podstaw obu stożków, brakuje nam natomiast ich wysokości. Jeżeli oznaczymy
. Znamy promienie podstaw obu stożków, brakuje nam natomiast ich wysokości. Jeżeli oznaczymy 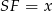 to możemy
to możemy  wyliczyć z podobieństwa trójkątów
wyliczyć z podobieństwa trójkątów 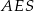 i
i 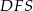 . Mamy
. Mamy
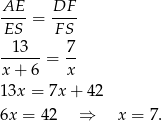
No i wszystko wiemy, więc liczymy objętość.
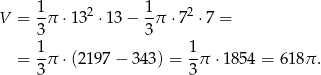
Odpowiedź: