/Szkoła średnia/Geometria/Stereometria

Zadanie nr 5193642

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa 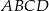ABCD jest trójkąt 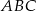ABC . Krawędź 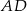AD jest wysokością ostrosłupa (zobacz rysunek).

PIC

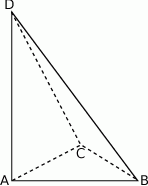
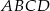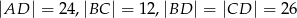Oblicz objętość ostrosłupa ABCD , jeśli wiadomo, że |AD | = 24,|BC | = 12,|BD | = |CD | = 26 .

Rozwiązanie

Podpiszmy długości krawędzi.

PIC

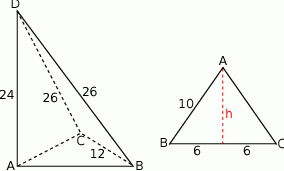
Z trójkąta prostokątnego 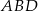ABD wyliczamy długość krawędzi podstawy AB .

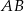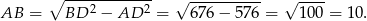
∘ ------------ √ ---------- √ ---- AB = BD 2 − AD 2 = 676 − 576 = 100 = 10 .

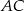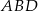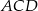Dokładnie taka sama jest długość odcinka AC (bo trójkąty ABD i ACD są przystające).

Zatem w podstawie mamy trójkąt równoramienny o ramionach długości 10 i podstawie długości 12. Rysujemy go z boku i liczymy długość jego wysokości opuszczonej na bok 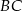BC .

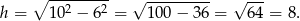
∘ --------- √ --------- √ --- h = 102 − 62 = 100− 36 = 64 = 8.

Zatem pole podstawy jest równe

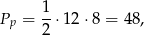
Pp = 1-⋅12 ⋅8 = 48, 2

a objętość ostrosłupa jest równa

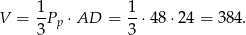
1 1 V = --Pp ⋅AD = -⋅ 48⋅2 4 = 384. 3 3

 
Odpowiedź: 384

Wersja PDF