/Szkoła średnia/Geometria/Stereometria

Zadanie nr 5210355

Dodaj do ulubionych
Dodaj do rozwiązanych

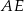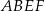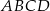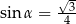W graniastosłupie prawidłowym trójkątnym krawędź podstawy ma długość 4, a przekątna AE , ściany ABEF jest nachylona do ściany ABCD pod kątem ostrym α takim, że √ - sin α = --3 4 .

PIC

  • Zaznacz na rysunku kąt α .
  • Oblicz objętość graniastosłupa.

Rozwiązanie

Wykonujemy rzut prostokątny wierzchołka E na podstawę ABCD i zaznaczamy kąt α .

PIC

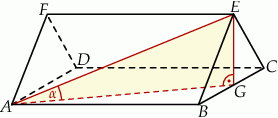
Graniastosłup jest prawidłowy, więc w podstawie ma trójkąt równoboczny. Zatem wysokość tego trójkąta jest równa

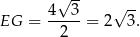
√ -- 4--3- √ -- EG = 2 = 2 3.

Korzystamy z informacji o sinusie kąta α i obliczamy długość przekątnej AE .

EG-- sinα = AE √ -- AE = -EG-- = 2√-3-= 8 . sin α -3- 4

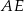Z twierdzenia Pitagorasa obliczamy długość krawędzi AB (wysokości graniastosłupa).

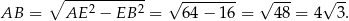
∘ ---2------2 √ -------- √ --- √ -- AB = AE − EB = 64 − 16 = 48 = 4 3.

Teraz możemy już obliczyć objętość

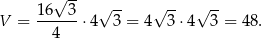
√ -- √ -- √ -- √ -- V = 16--3-⋅4 3 = 4 3 ⋅4 3 = 48 . 4

 
Odpowiedź: 48

Wersja PDF