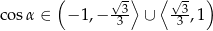/Szkoła średnia/Geometria/Stereometria

Zadanie nr 5337677

Dodaj do ulubionych
Dodaj do rozwiązanych

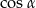Sześcian przecięto płaszczyzną przechodzącą przez przekątną podstawy. Płaszczyzna ta tworzy z podstawą kąt α . Dla jakich wartości cos α otrzymany przekrój jest trójkątem?

Rozwiązanie

Wystarczy sobie naszkicować opisaną sytuację i widać, że graniczne sytuacje są gdy opisana płaszczyzna (powiedzmy, że zawiera przekątną 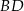BD ) przechodzi przez wierzchołki 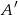A ′ i C ′ .

PIC

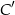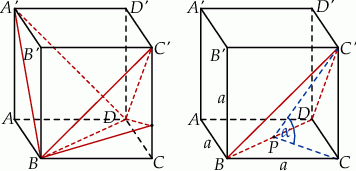
Spróbujemy teraz ustalić jakim kątom odpowiadają te sytuacje.

Jeżeli popatrzymy na trójkąt prostokątny 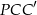PCC ′ , gdzie 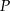P środek podstawy, to 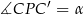∡CP C′ = α zatem

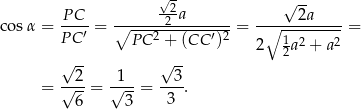
√ - PC --2a √ 2a cos α = ---- = ∘------2-------- = -∘-----------= P C′ P C2 + (CC ′)2 2 1a2 + a2 √ -- √ -- 2 2 1 3 = √---= √---= -3-. 6 3

Zauważmy, że łatwo ustalić jaki jest kąt 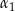α1 w drugim ze skrajnych przypadków, gdy płaszczyzna przechodzi przez punkt 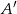′ A . Jeżeli oznaczymy przez 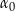α 0 przed chwilą wyliczony kąt, to mamy

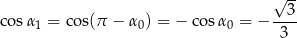
√ -- --3- cosα1 = cos(π − α0) = − cosα 0 = − 3

Widać więc, że przekrój będzie trójkątem dla 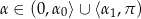α ∈ (0 ,α 0⟩∪ ⟨α1,π ) . Jeżeli naszkicujemy sobie funkcję 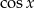cos x , to widać, że odpowiada to warunkowi

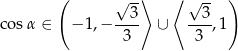
( ⟩ ⟨ ) √ 3- √ 3- co sα ∈ − 1,− ---- ∪ ----,1 3 3

 
Odpowiedź: ( √-⟩ ⟨ √ - ) c osα ∈ − 1,− -3- ∪ --3,1 3 3

Wersja PDF